密度推定を用いた回帰

今回は，特に実用性はないけど，回帰をより深く理解するためにはいいかもしれない，密度推定（Density Estimation）を用いた回帰というのを紹介したいと思う． まず，回帰は「条件付き確率の期待値」を求めるという枠組みだ． フォーマルに書くと，入力を$x$，出力を$y$とすると，以下の関数$f$を求めるのが回帰である．

$$\begin{align*} f(x) = \mathbb{E}_{y \sim p(y|x)} \left[y\right] = \int y p(y|x) dy \end{align*}$$

ここで，「右の積分はどうやって計算するんだ？」という疑問が生まれる． $p(y|x)$の形によっては，上の関数を解析的に求めることが可能だが，そうではない場合ももちろんある． こういう場合は，例えば，期待値をサンプリングにより近似する，重点サンプリング（importance Sampling）という手法で計算できる． 重点サンプリングでは，代理分布$p'(x)$を用いて，上記の積分を以下のようにサンプル近似する．

$$\begin{align*} \int y p(y|x) dy = \int y \frac{p(y|x)}{p'(y)} p'(y) dy \approx \frac{1}{n} \sum_{i=1}^n y_i \frac{p(y_i|x)}{p'(y_i)} =: \hat{f}(x) \end{align*}$$

ただし，$\{y_i\}_{i=1}^n \sim p'(y)$である． つまり，代理分布$p'(y)$にサンプリング可能な（乱数を生成できる）確率密度関数を持って来ればいいというわけだ． ここで，重み$w_i (x)$を以下のように定義する．

$$\begin{align*} w_i (x) := \frac{p(y_i|x)}{p'(y_i)} = \frac{p(x, y_i)}{p(x) p'(y_i)} \end{align*}$$

上の式からわかるように，$p(x, y)$と$p(y)$が推定できれば，上の重みは計算できる． というわけで今回はこれをカーネル密度推定（Kernel Density Estimation, KDE）で推定してみる．

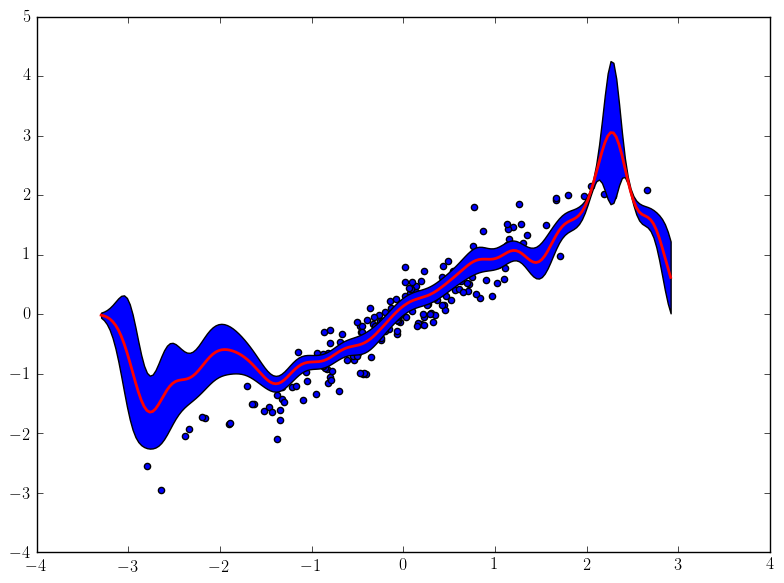
では，実験してみる．結果は以下のようになった．青い点がサンプルで，赤い線が推定した関数$f$である． ちなみに，この手法だと分散$\sigma^2(x) = \mathbb{E}_{y \sim p(y|x)}\left[(y - \mu(x))\right]$も計算できるので，それも合わせてプロットしてみた． みればわかるように，サンプルが少なくて推定結果が曖昧なところでは分散が高くなっている．なお，コードは記事の最後に添付する．

今回は密度推定を用いた回帰というのを紹介してみた． これを使えば，実は，Baysian Optimizationぽいことができるので，次はそれについて書きたいと思う．