ソフトマージンSVMのヒンジ損失最小化学習としての解釈とその実装

前回，ハードマージンSVMの定式化について書いたので， 今回はソフトマージンSVMの定式化をしようと思います． さらに，それをヒンジ損失最小化学習として解釈できることを示し， 最後に確率的勾配法を使って実装したいと思います．

さて，ハードマージンSVMの最適化問題は以下で与えられます．

$$\begin{align*} \min_{\boldsymbol{w},b} &\ \|\boldsymbol{w}\|^2 \\ s.t. &\ y_i(\boldsymbol{w}^T \boldsymbol{x}_i + b) \geq 1 \ \forall i=1,\ldots,n \end{align*}$$

しかし，与えられたデータに対して，この制約を満たす超平面が存在しない場合，実行可能領域が空集合となり，この最適化問題が解を持たなくなってしまいます． そこで，制約を緩和するために，全てのサンプルに対して$\xi_i \geq 0$を導入し，最適化問題を以下のように書き換えます．

$$\begin{align*} \min_{\boldsymbol{w},b,\{\xi_i\}_{i=1}^n} &\ \|\boldsymbol{w}\|^2 + C \sum_{i=1}^n \xi_i\\ s.t. &\ y_i(\boldsymbol{w}^T \boldsymbol{x}_i + b) \geq 1-\xi_i \ \forall i=1,\ldots,n\\ &\ \xi_i \geq 0 \ \forall i=1,\ldots,n \end{align*}$$

これは，訓練データでの誤識別をある程度許容することに相当します． 我々のゴールは汎化能力の獲得，つまり，未知のデータに対する誤識別率を最小化することなので，訓練データを全て正しく識別する必要はありません． さらに，訓練データに完全にフィットさせることは，汎化能力の低下を引き起こす原因にもなります．そのような意味でも，制約の緩和は有用です．

この最適化問題では，$\xi_i>0$の時，$\boldsymbol{x}_i$の誤識別を許容します． さらに，$\xi_i$は小さい方が望ましいので，目的関数に加えて同時に最小化します． $C$は識別率をコントロールするハイパーパラメータです．

さて，ここで，$\xi_i$を以下のように定義すると，

$$\begin{align*} \xi_i = \max\{0,1-y_i(\boldsymbol{w}^T \boldsymbol{x}_i + b)\} \end{align*},$$

上の最適化問題は，以下のように書き換えられます．

$$\begin{align*} \min_{\boldsymbol{w},b} \ \sum_{i=1}^n \max\{0,1-y_i(\boldsymbol{w}^T \boldsymbol{x}_i + b)\} + \lambda \|\boldsymbol{w}\|^2 \end{align*}$$

ここで，$\max\{0,1-y_i(\boldsymbol{w}^T \boldsymbol{x}_i + b)\}$を損失関数とみると，経験リスク最小化学習になっていることがわかります．損失関数$\ell_{hinge}(t) = \max\{0,1-t\}$はヒンジ損失と呼ばれています．

ここから実装について，書きたいと思います． オンライン機械学習 (機械学習プロフェッショナルシリーズ)を参考にしています． SVMは二次計画法で解くこともできますが，今回は確率的勾配法（正確にはIncremental Gradient Method）を使って解きたいと思います． $\boldsymbol{x} \in \mathbb{R}^{d+1}$ として，簡単のために $x_1 = 1$とします．すると，切片$b$が$\boldsymbol{w}$に吸収され，上の最適化問題は，

$$\begin{align*} \min_{\boldsymbol{w},b} \ \sum_{i=1}^n \max\{0,1-y_i\boldsymbol{w}^T \boldsymbol{x}_i\} + \lambda \|\boldsymbol{w}\|^2 \end{align*}$$

と書けます． 確率的勾配法では，適当にサンプル$(\boldsymbol{x}_i,y_i)$を一つ取り出して，それに対応する目的関数，

$$\begin{align*} J_i(\boldsymbol{w}) = \max\{0,1-y_i\boldsymbol{w}^T \boldsymbol{x}_i\} + \lambda \|\boldsymbol{w}\|^2 \end{align*},$$

の勾配を求めます．その勾配$\nabla J_i(\boldsymbol{w})$を用いて，パラメータを$\boldsymbol{w} \leftarrow \boldsymbol{w} - \eta\nabla J_i(\boldsymbol{w})$と更新します．これを収束まで繰り返します．

しかし，ヒンジ損失は$1-y_i\boldsymbol{w}^T \boldsymbol{x}_i = 0$を満たす点で微分不可能なため，劣勾配を考えます．

$$\begin{align*} \nabla J_i(\boldsymbol{w}) = \left\{ \begin{array}{ll} -y_i\boldsymbol{x}_i + 2 \lambda \boldsymbol{w} & (1-y_i\boldsymbol{w}^T \boldsymbol{x}_i \geq 0) \\ 2 \lambda \boldsymbol{w} & otherwise \end{array}\right. \end{align*}$$

これを踏まえると，アルゴリズムは以下のようになります．

1. ランダムに$(\boldsymbol{x}_i,y_i) \in \{(\boldsymbol{x}_i,y_i)\}_{i=1}^n$を取り出す．
2. 以下のように$\boldsymbol{w}$を更新 ($\eta$はステップサイズ)

$$\begin{align*} \boldsymbol{w} \leftarrow \boldsymbol{w} - \eta\left(2 \lambda \boldsymbol{w} + \left\{ \begin{array}{ll} -y_i\boldsymbol{x}_i & (1-y_i\boldsymbol{w}^T \boldsymbol{x}_i \geq 0) \\ 0 & otherwise \end{array}\right.\right) \end{align*}$$

実装してみました．

結果は以下のようになりました．

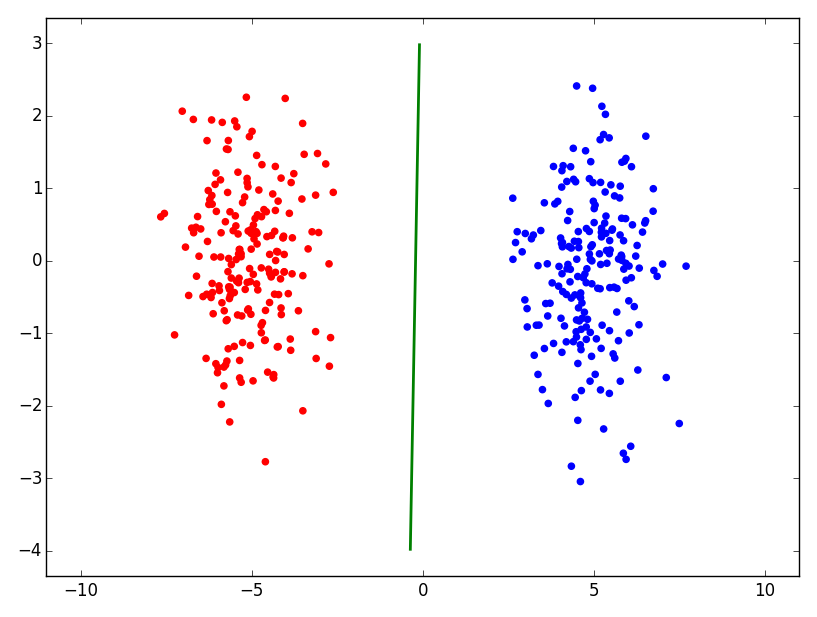
なお，以下に書いたように，実装においてはステップサイズの決定が非常に難しいです．

• 勾配法で目的関数値は単調に減少していくのか？

実際に使用する時は，scikit-learnのsklearn.linear_model.SGDClassifierを使うのが賢明でしょう．

• http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.SGDClassifier.html

今回はソフトマージンSVMを定式化し，確率的勾配法を用いて実装してみた． とりあえず簡単な人工データでうまく動くことを確認した． この実装は実用に耐えうるものではないので，簡単なデモだと思ってください^^． 読んでいただき，ありがとうございました．