正例とラベル無しデータからの学習 (PU classification)

通常の2値分類問題では，正例と負例が与えられています． しかし扱う問題によっては，このようなデータを用意するのが困難な時があります． 例えば，抽出型のタスクです． 抽出型のタスクでは，抽出したい対象を正例と考えます． この場合の負例は「正例以外のデータ」と定義するほかありません． しかし，集めた正例に対し，それ以外のデータを負例と定義してしまうと， それ以外のデータに含まれる正例も負例として扱ってしまいます．

このように負例を定義するのが難しい場合には，正例とラベルなしデータから学習する枠組み，PU classificationが有用です． PU classificationについては，Elkan and Noto 2008を参照していただければと思うのですが，少しだけ解説しておきます． 3つの確率変数$x,y,s$を考えます．ここで，$x \in \mathbb{R}, y \in \{-1,1\}, s \in \{0,1\}$だとします． $x$は入力，$y$はクラスラベル，そして$s$はデータがラベリングされるかどうかを表しています． 我々が欲しいのは， $p(y|x)$ ですが，PU classificationでは$y$は観測することができません． 我々のゴールは，$\{(x_i,s_i)\}_{i=1}^n$から $p(y|x)$ を学習することです． 結果からいうと，2つの仮定をおくことで，

$$p(y=1|x) = \frac{p(s=1|x)}{p(s=1|y=1)}$$

と表せます． $p(s=1|x)$ は与えられたデータから推定できます． そして， $p(s=1|y=1)$ は開発データから推定できます． 詳しくはElkan and Noto 2008の2章にまとめられています． 今回はElkan and Noto 2008の手法を用いてPU classificationを行っていきます．

では，以下のような正解データを考えましょう．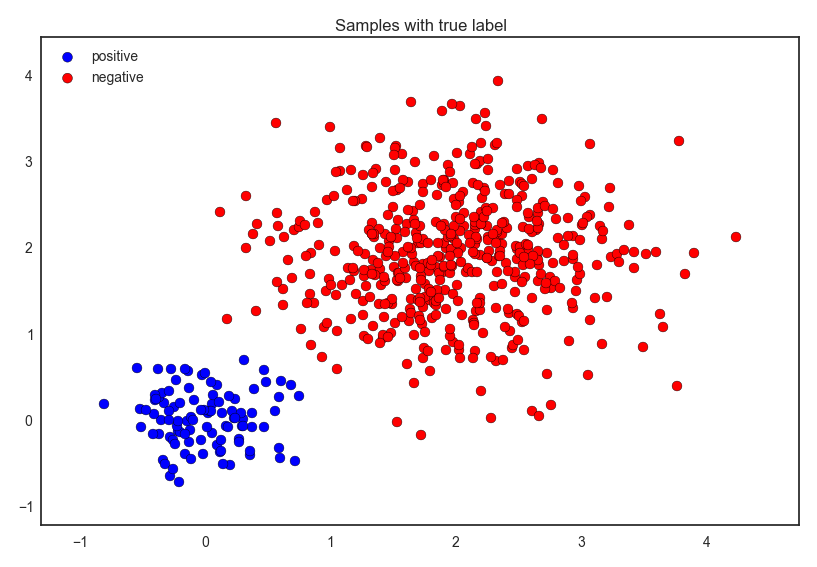

このデータに対して，実際に与えられるのは以下のようなデータです．

このデータに対して，まずは通常のロジスティック回帰を適用してみます． なお，今回は負例が多いので，交差確認法には正例側のF値を用います． 結果は以下のようになりました．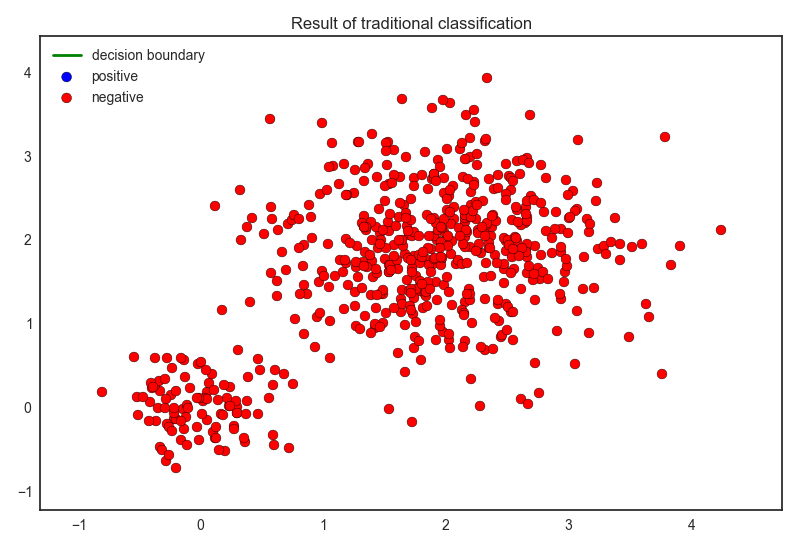

ご覧のように，全て負例だと予測してしまいました． 次に，PU classificationを適用してみます．

正例とラベルなしデータから，うまく分類境界を学習できていることがわかります．

デモ用のコードは以下に載せておきますのでぜひ試してみてください． ちなみに，非線形な分類境界を表現するためのrbfmodel_wrapper.py と PU Classificationのためのpuwrapper.py も合わせてDLしてください．

https://gist.github.com/nkt1546789/e9421f06ea3a62bfbb8c