平均値の差の検定の威力たるや...
Source and explanation
# coding: utf-8 """ 検定の威力を検証する. 今回は累積分布関数が人の目で見て非常に似ているケースを想定したい. なぜなら,累積分布関数が明らかに違うなら,検定を行う必要もないと思うからだ. 二つの分布から生成された標本x1, x2がある. それぞれの平均値mmu1, mmu2を使って,x1,x2は別々の分布から生成されたことを検定で確かめる. 帰無仮説:x1,x2は同じ分布から生成された. この仮説を棄却できるかどうかを調べる. なお,分布には正規分布を使い,真のパラメータはそれぞれ(mu1, sigma1), (mu2, sigma2)である. """ import numpy as np import random class Cdf(object): def __init__(self, t): self.t = t self.N = float(len(t)) def prob(self, x): return len([tt for tt in self.t if tt <= x]) / self.N # 設定 # 大きさは1000ずつ n, m = 1000, 1000 # 真のパラメータ mu1, mu2 = 0, 1 sigma1, sigma2 = 1, 1 # 標本の生成 x1 = np.random.normal(mu1, sigma1, n) x2 = np.random.normal(mu2, sigma2, m) # 帰無仮説用 x = x1 + x2 #random.shuffle(x) # 標本平均 mmu1, mmu2 = x1.mean(), x2.mean() # 平均差 # この平均差が偶然なのかどうか調べる. delta = abs(mmu1 - mmu2) print print "n:", n print "m:", m print "mu1:", mmu1 print "mu2:", mmu2 print "delta:", delta # 1000回リサンプリングして1000個の平均差を得る. # 帰無仮説に基づくものなので,x1とx2を混ぜ合わせたものを使う. iters = 1000 deltas = np.array([np.mean([random.choice(x) for i in range(n)]) - np.mean([random.choice(x) for i in range(m)]) for i in range(iters)]) print '(Mean, Var) :', (deltas.mean(), deltas.var()) # 標本の平均差以上の平均差が生成される確率(p値)を計算. # 累積分布関数を使っているが,別に使わなくても良い. cdf = Cdf(deltas) left = cdf.prob(-delta) right = 1.0 - cdf.prob(delta) pvalue = left + right print 'Tails (left, right, total):', left, right, left+right # p値を見て判断 # plot用データ作成 cdf1 = Cdf(x1) cdf2 = Cdf(x2) minimum = np.min([x1.min(), x2.min()]) maximum = np.max([x1.max(), x2.max()]) px = np.linspace(minimum, maximum, 200) py1 = np.array([cdf1.prob(xx) for xx in px], dtype=float) py2 = np.array([cdf2.prob(xx) for xx in px], dtype=float) import matplotlib.pyplot as plt plt.plot(px, py1, "b-") plt.plot(px, py2, "b-") plt.show()
Results
Case 1: 全く同じ分布(パラメータ)
平均0分散1の正規分布と平均0分散1の正規分布から生成されたデータ. 累積分布関数はこんな感じ.見た目はほとんど同じ. こいつのp値は0.468で帰無仮説は棄却できない. つまり,同じ分布から生成されたということ.理にかなう. 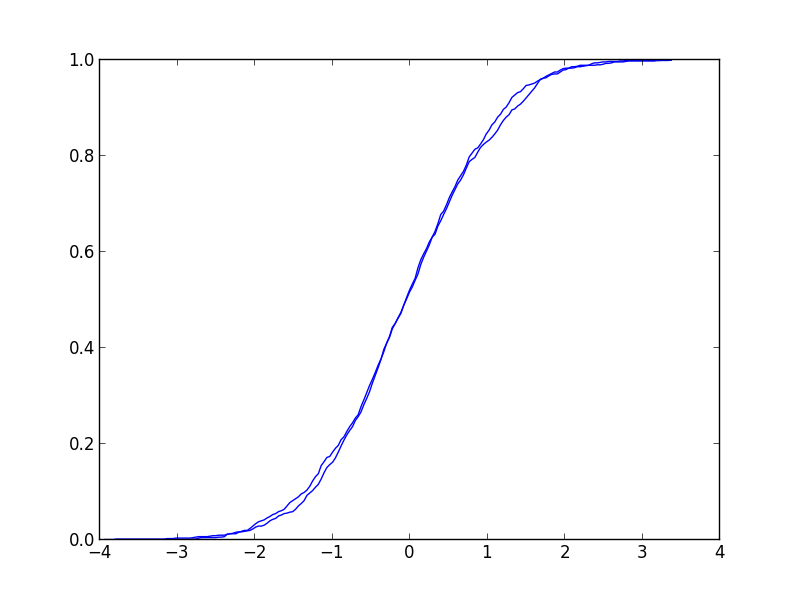
Case 2: ほぼ同じ分布(パラメータ)
平均0分散1の正規分布と平均0.15分散1の正規分布から生成されたデータ. 累積分布関数はこんな感じ.さきほどまではいかないが見た目はほとんど同じ. p値は0.049で,有意水準5%でなら棄却できる.(使い方あってるのか…) 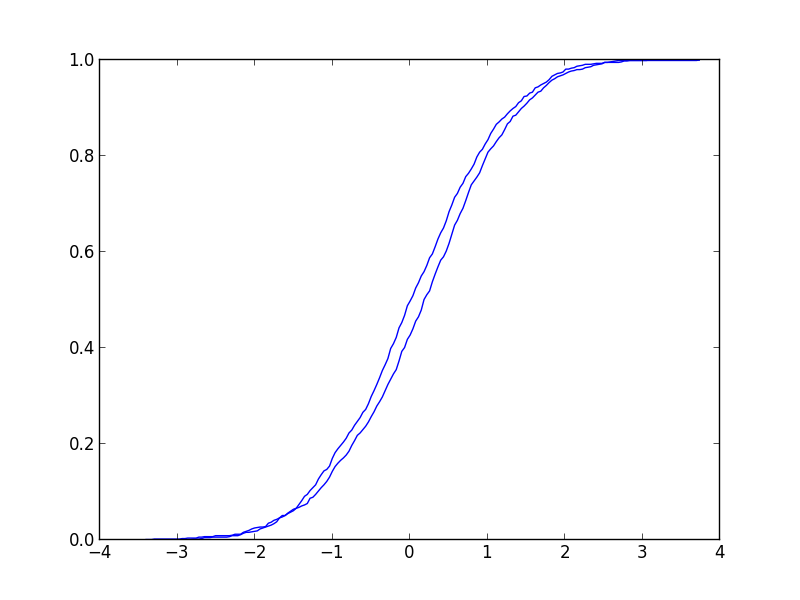
Case 3: 異なる分布(パラメータ)
平均0分散1の正規分布と平均1分散1の正規分布から生成されたデータ. 累積分布関数はこんな感じ.見た目から同じ分布(同じパラメータ)から生成されていないことがわかる. 是非棄却されてほしい. 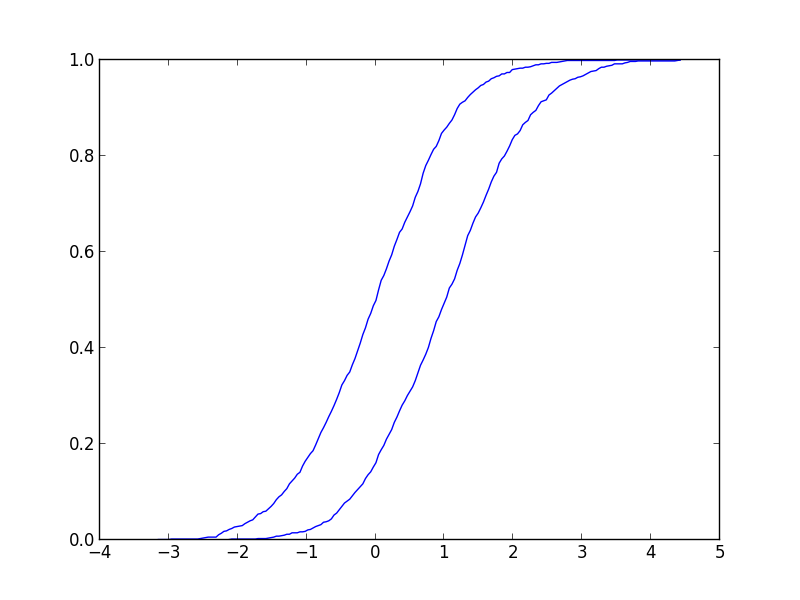 p値は0で期待通り棄却できる.
p値は0で期待通り棄却できる.
Summary
平均値の検定は,2つのデータがあり,それぞれ異なる分布(あるいはパラメータ)から生成されたかどうかを確かめることができる. 今回は同一分布(正規分布)で,パラメータだけを変えて実験をしてみた. 検定結果は理にかなっており,パラメータが全く同じなら,帰無仮説は棄却できず, パラメータを大きく変化(1程度)させると帰無仮説は棄却され,異なる分布と判断した. 問題は人間の目でみて,ほとんど同じだけどどうだろう?というケース(Case2). このケースを実験することで,「判断は,有意水準に委ねる」という統計学の非常にスマートな態度を実感することができた. これからの研究活動に役立ちそうだ.