KDEを使った相互情報量の推定

カーネル密度推定（Kernel density estimation）はノンパラメトリックな確率密度関数の推定法である。相互情報量（Mutual Information）の推定には、これを用いるのが最も基本的な方法である。確率変数 $X, Y$ 間の相互情報量は次式で定義される。

$\begin{align*} \int_X \int_Y p(x, y) \log \frac{p(x, y)}{p(x)p(y)} dxdy \hspace{5em} (1) \end{align*}$

ご覧のように、積分が出てきているので、まずはこれを潰さなければならない。ここには前回、前々回で使ったサンプル平均の考え方を用いる。さらに各確率密度関数を推定する必要があるが、今回は上述のようにカーネル密度推定により達成する。最終的に、以下のように相互情報量を推定する。

$\begin{align*} \hat{MI}(X, Y) := \frac{1}{n} \sum^n_{i=1} \log \frac{\hat{p}(x_i, y_i)}{\hat{p}(x_i)\hat{p}(y_i)} \end{align*}$

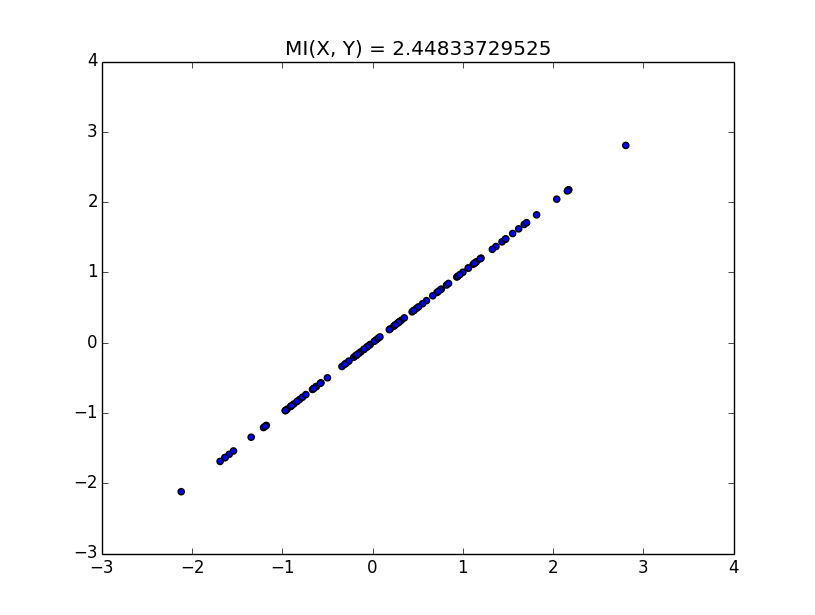
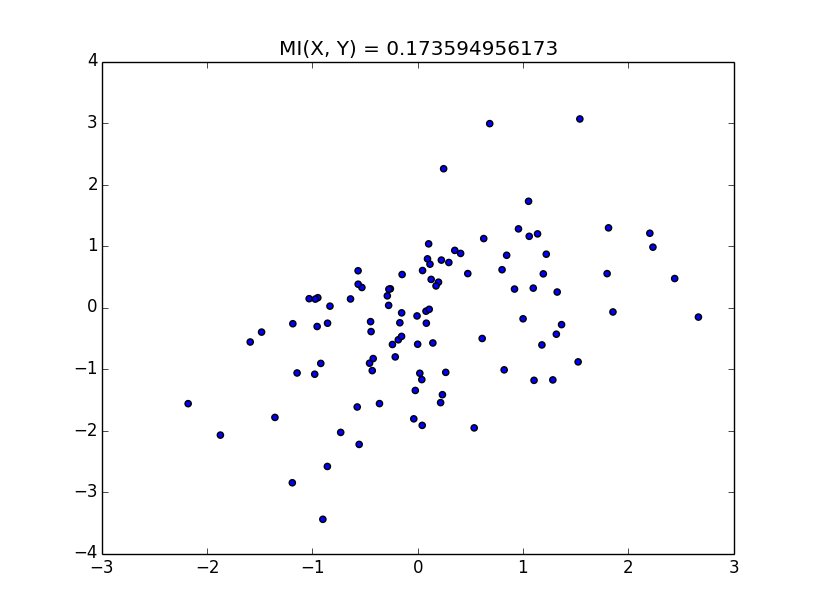
実行結果を以下に示す。これは真の値は出せていないので、簡単な例で解釈する。 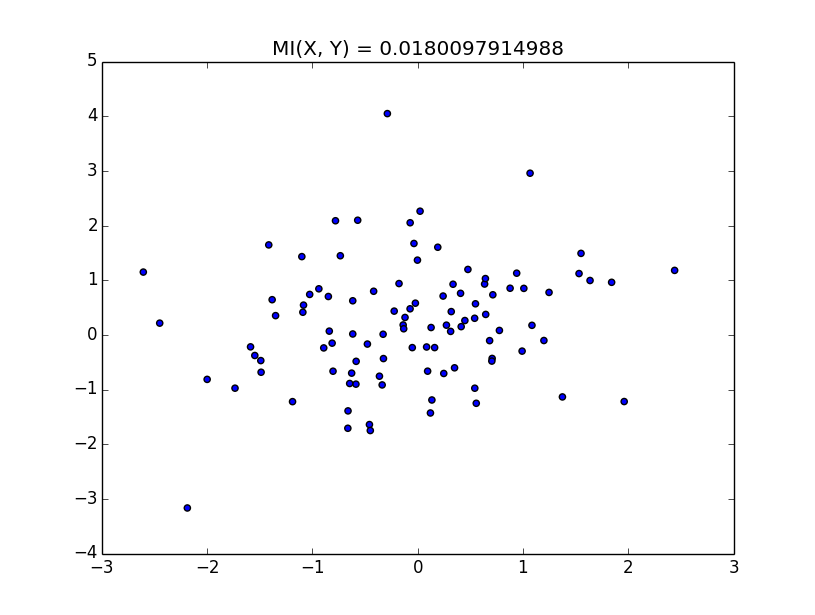file://c:/Users/Hiroyuki/Dropbox/nkt1546789.github.io/python_ml/MI_1.png このように、ｘとｙになんらかの相関がある場合、相互情報量は高くなる。逆になんの相関も無いならば、相互情報量は低くなる。しかし、単に相関を測るなら相関係数で良いじゃないか、となる。一般に普通の相関係数は線形な相関しか測れない。非線形な相関を測りたいならば、相互情報量が有用だ、という話を聞いたことがあるのでその辺りを次回確認したい。さらに、相関係数の非線形バージョンもあるみたいなので、その辺りも調べて行きたい。実験に使ったコードを以下に示す。

import numpy as np
import pylab as pl
from scipy import stats
from sklearn.neighbors import KernelDensity
from sklearn.grid_search import GridSearchCV
from sklearn import metrics

n = 100
mean = [0, 0]
cov = [[1, 0.4], [0.4, 1]]
x = stats.multivariate_normal.rvs(mean=mean, cov=cov, size=n)

params = {"bandwidth": np.logspace(-1, 1, 100)}
kde_xy = GridSearchCV(KernelDensity(), params).fit(x).best_estimator_
kde_x = GridSearchCV(KernelDensity(), params).fit(np.c_[x[:,0]]).best_estimator_
kde_y = GridSearchCV(KernelDensity(), params).fit(np.c_[x[:,1]]).best_estimator_

MI = np.sum(kde_xy.score_samples(x) - kde_x.score_samples(np.c_[x[:,0]]) - kde_y.score_samples(np.c_[x[:,1]]))/n
pl.scatter(x[:,0], x[:,1])
pl.title(&quot;MI(X, Y) = {0}&quot;.format(MI))
pl.show()