列空間（像）と零空間（核）と正射影行列

今読んでいる論文で重要な概念なので勉強し直しました． 理解に半日かかりました． 途中まで理解できたと思うので忘れないうちに．

行列 $A = [a_1|\cdots|a_n] \in \mathbb{R}^{m \times n}$ を考えます．

Aの列空間$C(A)$は文字通り列ベクトルで張られる空間です． 正確にはピポット列たちで張られる空間ですがここではAはフルランクだとします:

$$\begin{align*} C(A) := span\{a_1,\ldots,a_n\} \end{align*}$$

便宜上$A^T$の零空間$N(A^T)$を考えます．

$$\begin{align*} N(A^T) := \{x|A^T x= 0 \} \end{align*}$$

さて，今回議論したいのは，元の空間$\mathbb{R}^n$から$A$の列空間および$A^T$の零空間への正射影行列はどんな形をしているのか，ということです． ここからは図がないと議論しにくいのですが…

まずはモチベーション．以下の線形方程式を考えます．

$$\begin{align*} Ax=b \end{align*}$$

これは解をもたないことがあります．どんな時でしょうか？ それは$b$が$C(A)$に入っていない時です． そこで，$b$を$b$に最も近い$C(A)$内の点$p$で置き換えてから，これを解くことを考えます． さて，$p$は$C(A)$内の点なので，$p=A\hat{x}$と書けます． 元の方程式の解$x$の代わりに，$p=A\hat{x}$の解$\hat{x}$を求めようということです．

ここで，「最も近い点」とはなんなのかという議論になります． それをここで定義しなければなりません．ここは定義なので納得できなければ，または問題によっては変えても問題はないというわけです．

—ここから例に入ります—

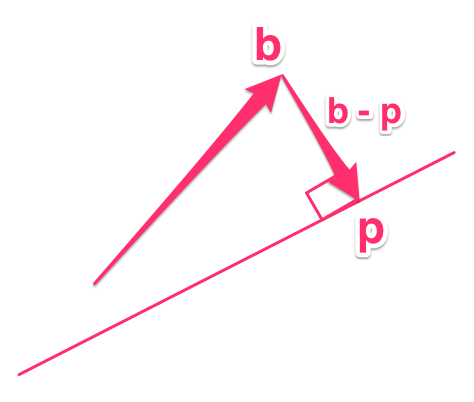
今，$A \in \mathbb{R}^{2\times 2}$とし，ランクは１とします． つまりこの線形変換により$\mathbb{R}^2$内の点は，ある直線上につぶされます． イメージを上に示します．図での直線が$C(A)$です． さて$A$には列が２つありますがそれらは線形従属の関係になっています． 上の図のように，$b$を$C(A)$に垂直に下ろした点をpと定義し，そのような射影,（これを正射影と呼ぶ）を$P$とします． 厳密に，$e:=b-p=b-A\hat{x}$とおくと，$e$と$C(A)$が直交するように$p$を定めます．

—ここまで例です—

$e$と$C(A)$が直交するという条件はつまり，$e$と$C(A)$の基底が直交するということです． $C(A)$の基底はAがフルランクならばその列からなる集合です． よって，$e$と$C(A)$が直交するという条件は以下のように書けます．

$$\begin{align*} A^T (b-A\hat{x}) = 0 \end{align*}$$

これより，

$$\begin{align*} \hat{x} = (A^T A)^{-1}A^T b \end{align*}$$

これで代わりの線形方程式が解けました． さらに，

$$\begin{align*} p=A\hat{x}=A(A^T A)^{-1}A^T b \end{align*}$$

ここから

$$\begin{align*} P = A(A^T A)^{-1}A^T \end{align*}$$

は$\mathbb{R}^n$の任意の要素$b$を$C(A)$に正射影する行列（正射影行列）だということが読み取れます．

さて，では$\mathbb{R}^n$から$N(A^T)$への正射影行列$Q$はどうやって求めるのでしょうか． 実は，$C(A)$と$N(A^T)$は直交しています． これは結構簡単に証明できます．

$x \in C(A), y \in N(A^T)$とします．このとき，

$$\begin{align*} x^T y = (Ax')^T y = x'^T Ay = 0 \end{align*}$$

よって，$C(A)$と$N(A^T)$は直交しています． さらに次元定理より

$\begin{align*} n = dim C(A) + dim N(A^T) \end{align*}$ なので，$C(A)$の基底が$k$個からなり，$N(A^T)$の基底が$\ell$個あるとすると，$k+\ell=n$となります． つまり，任意の$b \in \mathbb{R}^n$は，$p \in C(A), q \in N(A^T)$を用いて，

$\begin{align*} b = p + q \end{align*}$ と表せる．これを変形すると，

$$\begin{align*} q = b - p = b - A(A^T A)^{-1}A^T b = (I - A(A^T A)^{-1}A^T) b \end{align*}$$

よって，$\mathbb{R}^n$から$N(A^T)$への正射影行列$Q$は，

$$\begin{align*} Q = (I - A(A^T A)^{-1}A^T) \end{align*}$$

と表せる．

以下の講義でここに書いてあるようなことが学べます．というよりそっちを見ていただいた方がよいと思います． 自分整理のためのメモでしたー．

• https://www.youtube.com/watch?v=osh80YCg_GM